Todas as imagens utilizadas neste pequeno artigo foram retiradas do livro A Student's Guide to Maxwell's Equations, de Daniel Fleisch, um livro sucinto sobre os princípios do eletromangetismo. Uma referência completa sobre o assunto é o livro Engineering Electromagnetics, do autor Nathan Ida.

Lei de Gauss para campos elétricos

Esta lei define o campo elétrico gerado por cargas eletrostáticas no espaço. Consideremos neste primeiro momento, apenas o espaço livre (vácuo):

(forma integral)

ou

(forma diferencial)

Todas as equações de Maxwell podem ser escritas de duas maneiras diferentes: forma integral ou diferencial. Aquela as definem em uma região do espaço utilizando integrais e a diferencial; pontualmente, utilizando-se o operador del ou nabla (cálculo vetorial). Para maiores informações, consulte o artigo refere a Cálculo Vetorial.

Forma integral

A forma integral desta lei baseia-se na aplicação da definição matemática de fluxo elétrico em uma superfície fechada S:

Segundo a lei de Gauss, o fluxo elétrico resultante é numericamente igual à carga elétrica presente no volume definido pela superfície fechada da integral, dividido pela permissividade do espaço livre. Portanto, ela determina que nenhuma carga elétrica externa à superfície S pode alterar o fluxo elétrico líquido.

Devido à existência de uma integral de superfície, sua aplicação se restringe aos casos simétricos:

Distribuição espacial	Equação
Carga pontual
Linha infinita carregada
Plano infinito carregado

Sendo , a densidade linear de carga elétrica e , a densidade superficial de carga elétrica.

Forma diferencial

A forma diferencial define a mesma ideia de maneira local/pontual:

Dessarte, o campo eletrostático é divergente apenas nas regiões do espaço em que houver presença de carga elétrica.

Lei de Guass para campos magnéticos

Semelhante ao caso anterior, temos a definição do fluxo magnético no espaço:

(forma integral)

ou

(forma diferencial)

Forma integral

Novamente, aplica-se a definição matemática de fluxo de um campo vetorial em uma superfície fechada S:

Mas, ao contrário do caso anterior, o fluxo magnético resultante sob uma superfície fechada é nulo, independente de qualquer tipo de matéria presente no volume delimitado por ela:

Essa relação é consequência da estrutura do campo magnético: não há monopolos magnéticos na natureza. Portanto, não existe uma origem/fonte como uma carga elétrica pontual no caso dos campos elétricos:

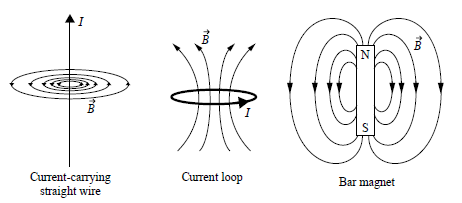
Esta lei é útil para solucionar problemas complexos, mas deve-se utilizar a lei de Biot-Savart para encontrar as relações de um campo magnético:

, de acordo com essa interpretação geométrica:

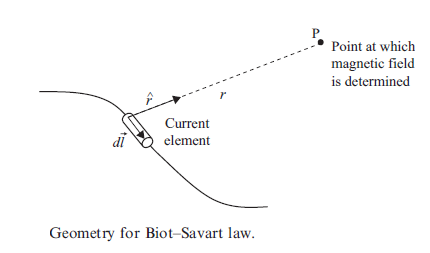
Forma diferencial

Temos a seguinte definição pontual da lei de Guass para o caso magnético:

Ou seja, temos um campo vetorial solenoidal.

Lei de Faraday

As formulações supracitadas apenas relacionam o campo elétrico com a distribuição de carga elétrica e o fluxo magnético em uma superfície fechada, respectivamente. A lei de Faraday é a primeira relação entre o campo elétrico e magnético (fenômenos distintos até então):

(forma integral)

ou

(forma diferencial)

Ou seja, temos a relação matemática do campo elétrico induzido a partir de um campo magnético variante no tempo.

Forma integral

Na forma integral temos que a integral de linha ao longo de uma curva fechada C é numericamente igual à derivada temporal do fluxo magnético em uma superfície não-fechada S qualquer que seja delimitada pela curva C.

O sinal negativo se refere à lei de Lenz. O sentido do campo elétrico e da consequente corrente induzida na matéria será tal que o campo magnético produzido por tal corrente tenderá a manter o fluxo magnético original externo, conforme a figura abaixo:

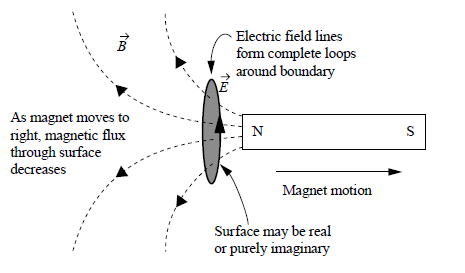
Ao contrário dos campos eletrostáticos, estes campos induzidos devem necessariamente formar curvas fechadas (caso b da figura abaixo). Portanto, não mais se originam de pontos no espaço, como ocorre nos campos produzidos por cargas pontuais (caso a):

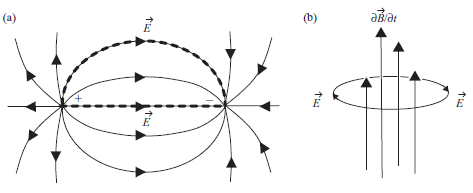
Perceba que a integral de linha do campo elétrico em função do deslocamento infinitesimal também é utilizada na definição da tensão elétrica:

(definição do potencial elétrico)

Entretanto, agora temos uma integral fechada e não podemos mais aplicar o conceito de diferença de potencial elétrico entre dois pontos distintos: apenas a concepção de energia necessária para mover uma carga elétrica ao longo do deslocamento; neste caso, uma curva fechada.

Forma diferencial

Empregando-se o cálculo vetorial, obtemos:

ou

Dessarte, temos um campo elétrico circulante no espaço gerado por um campo magnético variante no tempo.

Lei de Maxwell-Ampère

A quarta lei das equações de Maxwell define a relação restante entre o campo elétrico e o magnético: o campo magnético induzido por um campo elétrico variante no tempo, além da inclusão da lei de Ampère original. Confira:

(forma integral)

ou

(forma diferencial)

(forma integral)

Na realidade, temos duas fontes de campo magnético: uma corrente elétrica constante e um campo elétrico variante no tempo.

Forma integral

No lado esquerdo da equação na forma integral, temos a circulação do campo magnético ao longo da curva fechada C, conhecida por curva amperiana, e, no lado direito, o produto da permeabilidade magnética do espaço livre pela corrente elétrica englobada pela curva C e o produto da permissividade elétrica do espaço livre e a derivada temporal do fluxo do campo elétrico na superfície S.

Forma direrencial

Como sempre, temos uma equação mais sucinta e inteligível:

Sendo que o termo provém da lei de Ampère e o termo é conhecido por densidade da corrente de deslocamento, embora não consista em uma corrente elétrica no sentido estrito.

Sumário

Finalmente, temos as quatro equações fundamentais da teoria eletromagnética, usualmente denominadas equações de Maxwell, embora desenvolvidas por vários cientistas teóricos e práticos ao longo de várias décadas:

Embora tenhamos definido as equações apenas no espaço livre, elas também podem ser modificadas para descreverem todos os fenômenos eletromagnéticos que interajam com a matéria (polarização elétrica e magnética):

Sendo que os campos auxiliares e estão descritos no artigo Campos densidade elétrica (D) e intensidade magnética (H): relações constitutivas.

Ondas Eletromagnéticas

Essas equações sintetizam toda a teoria eletromagnética e culminam na equação de onda para campos magnéticos e elétricos (ondas eletromagnéticas) no vácuo:

e

Portanto, de acordo com a equação genérica da onda:

,

também conhecida por velocidade da luz.

Para maiores informações, consulte os livros: A Student's Guide to Maxwell's Equations, de Daniel Fleisch, e Engineering Electromagnetics, autor Nathan Ida.